Paseo por la calle y encuentro un cartel adosado a un semáforo que reza: “¡¡Atención!! Por su seguridad mantenga la distancia social (2 metros) ¡¡Circule por su derecha!!”
Si accedemos a un supermercado también nos encontramos varias señales de guardar la susodicha distancia de seguridad, sobre todo a la hora de guardar colas. En otros lugares, la distancia a obedecer es de un metro y medio. Para establecimientos pequeños es recomendable hacer colas en el exterior. Incluso en las playas tenemos que mantener las distancias.
El hecho es que las autoridades están recomendando la distancia social como el método más efectivo para reducir los contagios. Sobre todo en sitios cerrados. A estas alturas, toda la ciudadanía lo sabe.
Sin embargo, la Consejería de Educación de la Junta de Andalucía considera que puede realizarse una vuelta al cole normalizada: grupos burbuja, gel hidroalcohólico, personal de refuerzo… Ha publicado tanto unas instrucciones como unas aclaraciones al respecto, con las cuales no están de acuerdo la práctica totalidad de los sindicatos, muchas organizaciones de madres y padres, y bastantes directivas de centros, manifestándose todos los colectivos citados en varias ocasiones en contra de ellas. Y el argumento en contra más contundente es la ratio (número de alumnos por aula); si no se disminuye en un porcentaje significativo, no garantiza la distancia de seguridad y, por lo tanto, sometemos a la población escolar a un riesgo evidente. No sólo al alumnado, sino a todos los que lo rodean: familiares y personal docente y no docente de los centros.
Como profesor en un instituto de titularidad pública de esta ciudad, Jerez, en el que llevo quince años de docencia más otros años en otros centros, tengo una opinión. Pero no la voy a decir, ni mucho menos. Simplemente voy a exponer, en este artículo, lo que aún no he visto en ninguno: calcular, matemáticamente, cuántos alumnos o alumnas pueden entrar en un aula sin comprometer la distancia de seguridad de dos metros, la más recomendable. Voy a dejar que hablen las matemáticas. Y que cada cual saque sus propias conclusiones.
La ratio más normal en una clase de educación secundaria obligatoria es de treinta alumnos/as. Pocas veces nos encontramos algunos menos, muchas algunos más. Sin embargo, parece razonable usar el número treinta como base de los cálculos.
Tengo a mano los planos del instituto, pero casi no me hacen falta. He entrado muchas veces en un aula típica de mi centro, y, además he ostentado el cargo de coordinador TIC, con lo cual mover mesas, organizar espacios, y otras tareas de carácter técnico en las clases me son habituales. Y creo hacerme una idea muy ajustada de sus proporciones. Antes de redactar este artículo, y sin posibilidad ahora en agosto de acceder físicamente y medir un aula, pensaba que aproximadamente mide como mucho siete metros de ancha y nueve de larga. Midiendo en el plano a escala 1:500 (no es un plano muy fiable) el ancho es de 15 mm y 17 mm el largo, con lo que un simple cálculo me muestra que tendría 7.5 m de ancha y 8.5 m de larga. Según lo que estimaba, el área del aula sería ?????=7? ? 9? = 63?2 y según el plano ?????=7.5? ? 8.5? = 63.75?2 con lo cual parece lógico suponer que el área de un aula, redondeando por encima, es de ?????=64?2.
Una vez calculada el área disponible, tendremos que calcular el área de seguridad de cada persona en el aula. Para calcular este área por alumno/a, dibujaremos una circunferencia alrededor del mismo. El radio de la misma, un metro. Es como si le pusiéramos un hula-hoop de dos metros de diámetro a cada uno con él o ella en el centro.
¿Por qué el radio a la mitad de la distancia? Porque cuando juntemos a varios alumnos, si las circunferencias se tocan en puntos de tangencia, aseguraremos que cada cual estará a dos metros del otro. Pero mejor verlo en la figura 1.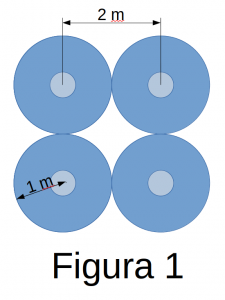
Luego el área de seguridad por alumno parece ser el área circular que lo circunscribe ???=?⋅?2=3.1416⋅(1?)2=3.1416 ?2. Pero no, es más. En la misma figura puede observarse que los cuatro círculos dejan un espacio vacío en su interior (figura 2, verde claro). Este espacio hay que añadirlo como parte del área de seguridad que necesito por alumno; no es un área que nos interese pero no podemos deshacernos de ella, por lo que hay que tenerla en cuenta. Así que su cálculo es el área del cuadrado que delimitan los cuatro alumnos de la figura 2 menos el área de cuatro sectores circulares a noventa grados (o sea,un círculo completo), lo cual nos da un área de: ????í?=?2−???=4?2−3.1416?2≃0.86?2.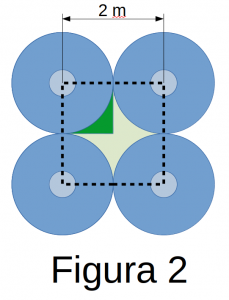
El área vacía que en la disposición de la figura 2 corresponde a un sólo alumno es un cuarto de la misma: 0.86?2/4 (en verde oscuro). Sin embargo, cada alumno está rodeado formando cuatro grupos de este tipo (figura 2B). Así que el área de seguridad efectiva por alumno es, en realidad: ???= 3.1416 ?2 + 4 ⋅0.86?2 / 4 ≃ 4?2 = ?2 , el área del cuadrado que lo circunscribe (en verde oscuro, figura 2B)
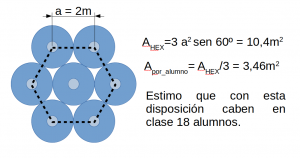
Puede haber quien piense que ese “área vacía” puede reducirse. Matemáticamente es posible una configuración del tipo “celda hexagonal”, pero entonces la disposición de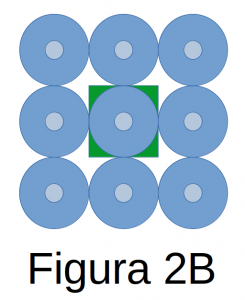 
las mesas y las sillas tiene que ser muy distinta a la habitual, no en filas y columnas, lo cual puede tener muy mal ajuste en una clase rectangular.
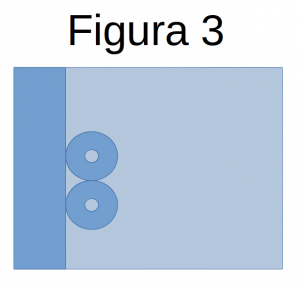Pensemos ahora en el docente. Normalmente se moverá en las explicaciones por la parte delantera de la clase, donde tiene su mesa y las pizarras, ya sean PDIs o normales. Su área de seguridad es una franja del ancho de la clase (supongo 7 m) por un metro, la mitad de la distancia de seguridad. Dispondremos al alumnado dentro del área en celeste claro - figura 3 -, con la primera fila de alumnos/as de manera que sus áreas de seguridad sean tangentes a la zona de seguridad del docente, y así guardarán con éste la distancia de dos metros.
Por tanto, si restamos al área del aula, ?????=64?2, el área de seguridad del docente ???=7? ⋅1? = 7?2, tenemos un área de aula efectiva para sentar al alumnado de ???=?????−???=64?2−7?²=57?2. Disponemos entonces de cincuenta y siete metros cuadrados, así que divido entre el área de seguridad de un alumno y…
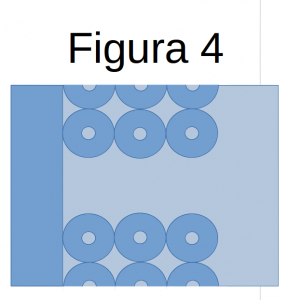No. Esto no es así. Hay que ser un poco más precisos. Si en clase tenemos normalmente 30 alumnos, en nuestro caso, cinco están pegados a la pared izquierda y cinco a la derecha. En el esquema de la figura 4 puede verse que con estos alumnos pegados a la pared sólo hay que tener en cuenta la mitad de sus áreas de seguridad.
También se podría razonar que el alumnado que se disponga al fondo de la clase puede aceptar asimismo la mitad del área de seguridad, pegando su espalda a la pared de atrás; pero lo condeno a no poder moverse. Así que no pienso considerarlo.
En definitiva, para calcular el área de seguridad total del alumnado, y suponiendo que tengo una ratio de treinta alumnos, y que diez de ellos estarán pegados a las paredes laterales, su área de seguridad será: ????????=10⋅(???⋅0,5) + 20 ⋅???=25 ⋅???=25 ⋅4?2 = 100?2. Hace falta, por tanto, una superficie efectiva para disponer el alumnado de cien metros cuadrados cuando en un cálculo anterior sólo dispongo de cincuenta y siete.
Si divido 57 entre 100, me sale que en porcentaje la disposición es del 57% del aforo. Aún necesito un 43% más de espacio de aula.
Si aplico el porcentaje al número de alumnos, 30 ⋅57% = 17,1, podré disponer de espacio para diecisiete.
Y esto considerando sólo un cálculo basado en áreas. Pero ya hemos visto que tenía espacios vacíos al intentar acomodar círculos en una disposición rectangular. Si queremos disponer alumnos en filas horizontales y columnas verticales, probablemente una fila no cabe justa en el ancho de la clase y una columna no cabe en el largo; por ejemplo, con el ancho, 7m / 2m = 3,5. Caben en un ancho una fila de 4 alumnos y medio, teniendo en cuenta uno más por lo del tema de pegarse a las paredes y razonando igual para el largo de la clase 9m / 2m = 4,5. Como no puedo hacer como Salomón y partir alumnos por la mitad, me quedan cuatro por cuatro, dieciséis.
El planteamiento del problema, considerando que no haya errores ni en los cálculos ni en su interpretación, no deja de ser una situación ideal. Más factores puede que haya que tener en cuenta. Por ejemplo, hay que considerar el mobiliario. Hay centros que pueden tener mesas para cada dos alumnos, de las que hace unos años tenían un ordenador de sobremesa para compartir, y en dichas mesas están sentados codo con codo. La situación, pues, sería otra más compleja.
Si alguien considera que dos metros es una exageración, encontrará una distancia en la que cabrán los treinta. Según mi hoja de cálculo, alrededor del metro y medio. ¿Es esto deseable?¿Es asumible?
Dejaré que el lector lo interprete y opine. Espero que este pequeño artículo le sirva para ayudarle a reflexionar sobre la cuestión.
Si quieren acceder a la hoja de cálculo, pueden escribirme a mi correo (aurelio@seritium.es) y con gusto les facilitaré una copia.
Comentarios